
問1 浮動小数点数に関する次の記述を読んで,設問1,2に答えよ。
(1) α ×2β の形で表記される浮動小数点数を,図1に示す 32 ビット単精度浮動小数点形式 (以下,単精度表現という)で表現する。ここで,αとβは次の条件を満たすものとする。
-126 ≦ β ≦ 127

図1 32 ビット単精度浮動小数点形式
αの値が正のとき 0,負のとき1が入る。
② 指数部(ビット番号 30 ~ 23 )
βの値に 127 を加えた値が2進数で入る。
③ 仮数部(ビット番号 22 ~ 0)
lαl の整数部分 1 を省略し,残りの小数部分が,ビット番号 22 に小数第1位が来るような2進数で入る。
(2) 例えば,10 進数の 0.75 を2進数で表すと,(0.11)2 となる。 これは (1.1)2 ×2-1 と表記でき,単精度表現では,図2のとおり,符号部は (0)2 ,指数部は-1に 127 を加えて (01111110)2 となり,仮数部は (1.1)2 の小数部分が入るので, (100…0)2となる。ここで,00…0 は 0 が連続していることを表す。

図2 0.75 の単精度表現
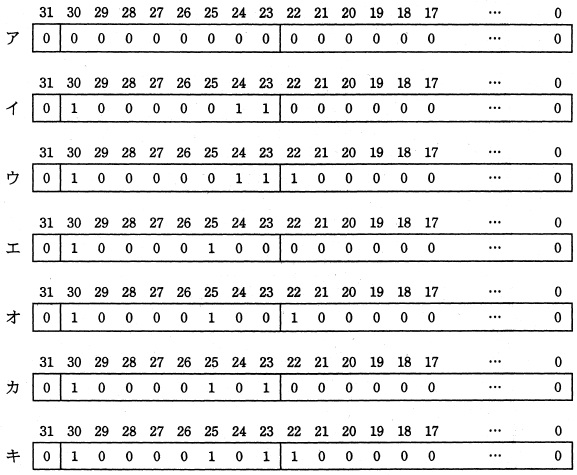
設問1 次の単精度表現が表す数値として正しい答えを,解答群の中から選選べ。

解答群
オ 11×2-125 カ 11×2-122 キ 11×25 ク 11×2132
設問2 次の記述中の
 に入れる正しい答えを,解答群の中から選べ。
に入れる正しい答えを,解答群の中から選べ。
二つの浮動小数点数 A と B の減算と乗算を行う。
A の単精度表現

B の単精度表現

(1) 減算 A-B を,次の手順①~③で行う。
① 指数部の値を大きい方に合わせる。A が(1.01)2×25 であることから,
B を (  )2 ×25 とする。
)2 ×25 とする。
② 減算を行う。
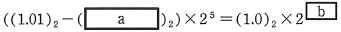
③ ②の結果を単精度表現する。その結果は  となる。
となる。
(2) 乗算 A×B の結果は (  ) 2×29 となる。
) 2×29 となる。
a に関する解答群
オ 1.1
オ 131 カ 132
オ 1.1111
[←前の問題] [次の問題→] [問題一覧表] [分野別] [基本情報技術者試験TOP ]
