
次のプログラムの説明及びプログラムを読んで,設問に答えよ。
鉄道の路線がある,駅数 N は2以上で,各駅には駅番号( 1,2,…,N )が付いている。 どの任意の2駅間にも,それらを結ぶ経路が一つ以上存在する。また, 隣接する2駅間を直接結ぶ経路は一つだけ存在し,その距離が与えられている。 図1に5駅からなる鉄道の路線例を示す。
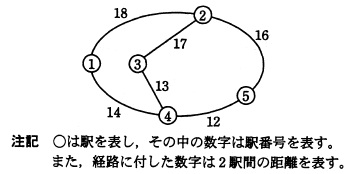
図1 鉄道の路線例 (1)
〔プログラムの説明〕
副プログラム CalcDist は,駅数 N 及び要素数 N×N の2次元配列 Dist を受け取り, プログラムに示すアルゴリズム(Warshall-Floyd 法)によって,配列 Dist の内容を 更新しながら各駅間の最短距離を求めていく。実行が終わると,任意の2駅 i,j 間の 最短距離が Dist[i][j] に求められている。どの2駅間についても, その最短距離は 999 より小さいものとする。配列 Dist の添字は1から始まる。
副プログラム CalcDist に渡す配列 Dist には,次の値を格納する。
なお,図1の路線情報を格納した配列 Dist の内容を,図2の初期値に示してある。
(1) 2駅 i,j が隣接しているとき,Dist[i][j] 及び Dist[j][i] には, その駅間距離を格納する。例えば,図1の駅①と②は隣接しているので, Dist[1][2] 及び Dist[2][1] には,18を格納する。
(2) 2駅 i,j が隣接していないとき,Dist[i][j] 及び Dist[j][i] には,未確定を 表す距離 999 を格納する。例えば,図1の駅①と③は隣接していないので, Dist[1][3] 及び Dist[3][1] には,999 を格納する。
(3) 各駅iについて,Dist[i][1] には0を格納する。
副プログラム CalcDist 中の Print(N,Dist) は,配列 Dist のその時点の内容を 印字する副プログラムである。
〔プログラム〕

図1の路線情報を配列 Dist に格納して,CalcDist を実行した。配列 Dist の内容の 変化を print(N,Dist) で印字した結果は,図2のとおりであった。

図2 配列 Dist の内容の変化を印字した結果
駅数 N に関して,副プログラム CalcDist の計算量のオーダは  ,また
メモリ使用量のオーダは
,また
メモリ使用量のオーダは  である。そこで,駅数 N が大きい場合に,
計算量やメモリ使用量を減らすための方法を考える。
である。そこで,駅数 N が大きい場合に,
計算量やメモリ使用量を減らすための方法を考える。
例えば,配列 Dist の対称性に着目し,プログラム中の  の部分を,
の部分を,
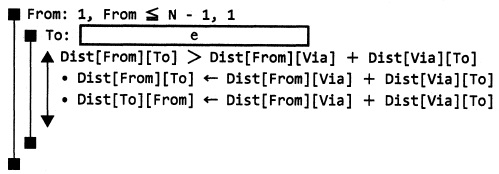
とすれば,繰返し処理中の選択処理の実行回数を約半分に減らすことができる。
次に,少ないメモリ使用量で,任意の2駅 i,j 間の最短距離を求める方法を考える。
駅を,乗換駅(3方向以上に隣接する駅がある),終端駅(1方向だけに隣接する駅がある), 中間駅(2方向だけに隣接する駅がある)の3種類に分ける。乗換駅と終端駅を 合わせて基幹駅と呼ぶ。基幹駅の数を K として,駅番号 1 ~ K が基幹駅, 駅番号 K+1 ~ N が中間駅となるように駅番号を定める。ここで,K≧2であるとする。 図3の路線例では,駅 ①~③が乗換駅,駅④が終端駅,駅⑤~⑩が中間駅である。
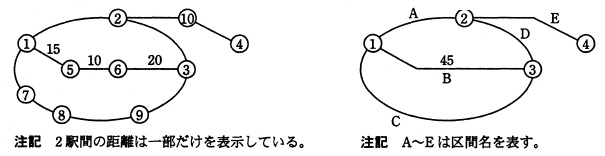
図3 鉄道の路線例 (2) 図4 鉄道の路線例 (2) の基幹駅区間名
各駅間の最短距離は,次の方法で求める。
(1) 中間駅を全て除いて,基幹駅だけからなる路線を考え,二つの基幹駅を結ぶ 経路ごとに一意の区間名を付ける。図3の路線例にこの操作を加えたものが図4である。 例えば,図3の経路①-⑤-⑥-③は,図4の区間Bに対応する。
(2) 要素数 K×K の2次元配列 Dist を用意し,事前に配列 Dist 各基幹駅間の 最短距離を求めておく。
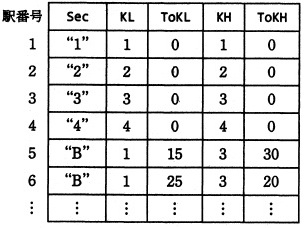
(3) 全ての駅について,表1に示す形式の駅情報表を用意する(表1には, 図3の駅情報の一部が示してある)。
中間駅の場合,Sec はその駅が属する区間の区間名,KL,KH はその駅が属する区間の 両端の駅番号( KL ≦ KH とする),ToKL,ToKH はその駅から駅 KL,KH までの距離である。 基幹駅の場合,その駅は自分自身の駅を両端とする距離0の区間に属すると考えて, 表1の例のように中間駅と同様の情報を用意する。
これらの情報は,駅番号を添字として参照する。 例えば,駅番号 5 の ToKL の値は ToKL[5] として参照する。
(4) 2駅 i,j 間の最短距離を求める。一般に,両駅が属する区間が異なる場合, 駅 i から駅 j へ行く経路は,
(駅 i )→(駅 i が属する区間のいずれか一端の基幹駅)
→(駅 j が属する区間のいずれか一端の基幹駅)→(駅 j )
となる,したがって,次の式で求める4通りの値 D1,D2,D3,D4 のうちの最小値が, 2駅 i,j 間の最短距離となる。
・D2 ← ToKL[i] + Dist[KL[i]][KH[j]] + ToKH[j]
・D3 ← ToKH[i] + Dist[KH[i]][KL[j]] + ToKL[j]
・D4 ← ToKH[i] + Dist[KH[i]][KH[j]] + ToKH[j]

この方法なら,2次元配列 Dist の要素数を N×N から K×K に削減できる。
ただし,表1に示す表が増えるので,例えば K=5 のとき,配列及び表が占めるメモリ使用量を
削減できるのは N ≧  の場合となる。ここで,表1に示す表は,
1駅について配列 Dist の要素5個分のメモリを使用するものとする。
の場合となる。ここで,表1に示す表は,
1駅について配列 Dist の要素5個分のメモリを使用するものとする。
設問 本文中及び図2中の  に入れる正しい答えを,
解答群の中から選べ。
に入れる正しい答えを,
解答群の中から選べ。
a,b に関する解答群
c,d に関する解答群
e に関する解答群
ウ From, To ≦ N - 1, 1 エ From + 1, To ≦ N , 1
f に関する解答群
イ (KL[i] ≠ KL[j]) or (KH[i] ≠ KH[j])
ウ Sec[i] = Sec[j]
エ Sec[i] ≠ Sec[j]
g に関する解答群
[←前の問題] [次の問題→] [問題一覧表] [分野別] [基本情報技術者試験TOP ]
