
〔プログラムの説明〕
画面上に凸四角形を描く関数 DrawRect を作成した。 関数 DrawRect は,次の大域変数を参照して動作する。
int Vx[4], Vy[4]; /* 4 頂点の座標値配列(Vx は x 座標, Vy は y 座標) */
ただし,第1頂点P1 から第3頂点P3 までは,画面上で時計回りになっており, その座標値は順番に Vx と Vy に格納されている。 画面上の座標系と原点の位置を図1に示す。
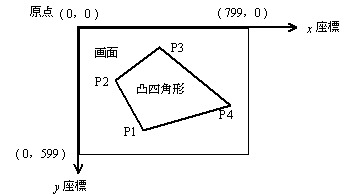
図1 画面上の座標系と原点の位置
第1頂点 P1 から第4頂点 P4 までは折れ線で結び, 次に第4頂点 P4 の位置を検査し,凸四角形になる場合には P4 とP1 を 結ぶ線分を描画して,返却値0を返す。 4頂点を結ぶ図形が,凸四角形ではなく,図2 に示すような図形となる場合には, P4 とP1 を結ぶ線分を描かずに,返却値−1 を返す。
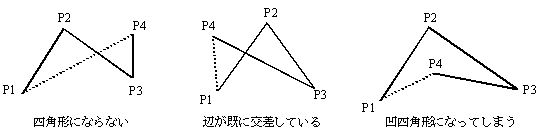
図2 凸四角形でない図形の例
なお,線分を引くために,次の二つの関数が用意されている。
void gMoveTo(int sx, int sy);
機能:線分の始点座標 ( sx, sy ) を設定する。この関数は描画を行わない。
void gLineTo(int ex, int ey);
機能:現在の始点から ( ex, ey ) まで線分を描き, 次の描画のために始点を ( ex, ey ) に更新する。
〔プログラム〕
void gMoveTo(int, int);
void gLineTo(int, int);
int nCheck(double a)
{
if (a > 0.0) return 1;
else if (a < 0.0) return -1;
return 0;
}
int DrawRect( )
{
int nCnt;
double dx, dy, k;
int nSide0, nSide1, nSide2;
for (nCnt = 0; nCnt < 4; nCnt++) {
if (nCnt == 0) gMoveTo(Vx[nCnt], Vy[nCnt]);
else if (nCnt < 3) gLineTo(Vx[nCnt], Vy[nCnt]);
else {
gLineTo(Vx[nCnt], Vy[nCnt]);
/* P3 と P4 を通る直線の方程式を求める。 */
dx = Vx[3] - Vx[2];
dy = Vy[3] - Vy[2];
k = dx * Vy[2] - dy * Vx[2];
/* 第1の判定 */
nSide0 = nCheck(dy * Vx[0] - dx * Vy[0] + k);
nSide1 = nCheck(dy * Vx[1] - dx * Vy[1] + k);
if (nSide0 != nSide1) return -1;
/* P4 と P1 を通る直線の方程式を求める。 */
dx = Vx[0] - Vx[3];
dy = Vy[0] - Vy[3];
k = dx * Vy[3] - dy * Vx[3];
/* 第2の判定 */
nSide1 = nCheck(dy * Vx[1] - dx * Vy[1] + k);
nSide2 = nCheck(dy * Vx[2] - dx * Vy[2] + k);
if (nSide1 != nSide2) return -1;
/* P3 と P1 を通る直線の方程式を求める。 */
dx = Vx[0] - Vx[2];
dy = Vy[0] - Vy[2];
k = dx * Vy[2] - dy * Vx[2];
/* 第3の判定 */
nSide1 = nCheck(dy * Vx[1] - dx * Vy[1] + k);
nSide2 = nCheck(dy * Vx[3] - dx * Vy[3] + k);
if (nSide1 * nSide2 != -1) return -1;
}
}
gLineTo(Vx[0], Vy[0]);
return 0;
}
設問1 関数 DrawRect は,描く図形が凸四角形かどうか調べるため,
直線の方程式を利用して辺の交差を判定している。
この処理に関する次の記述中の  に入れる正しい答えを,
解答群の中から選べ。
ただし,L12 は,第1頂点 P1 と,第2頂点 P2 を結ぶ線分を表す。
に入れる正しい答えを,
解答群の中から選べ。
ただし,L12 は,第1頂点 P1 と,第2頂点 P2 を結ぶ線分を表す。
2 点 P3 (x3,y3),P4 (x4, y4) を通る直線の方程式を求める。 この方程式は。 (x4 − x3)( y − y3) = (y4 − y3)( x − x3)
と表すことができる。 P4 と P3 の x 座標の差を dx, y 座標の差を dy とすると,。
dx = Vx[3] − Vx[2]
dy = Vy[3] − Vy[2]
である。この値を方程式に代入すると, dx( y − y3) = dy( x − x3)
となる。この式を展開すると,
dx × y − dx × y3 = dy × x − dy × x3
となる。ここで,定数をまとめて k とすると,直線の方程式は,
dy × x − dx × y + k = 0
と表すことができる。
定数 k は, x と y に  の座標値を代入すれば求めることができるので,求める直線の方程式は,
の座標値を代入すれば求めることができるので,求める直線の方程式は,
 = 0 となる。
= 0 となる。
凸四角形になるためには,P3 と P4 を通る直線と,線分 L12 が交差してはならない。
この交差を判定するため, の
x と y に,P1 と P2 の座標値を代入し,計算結果の
の
x と y に,P1 と P2 の座標値を代入し,計算結果の
 を比較して判定する。
を比較して判定する。
a,c に関する解答群
ア 第1頂点 P1 イ 第2頂点 P2 ウ 第3頂点 P3
エ 絶対値 オ 符号
b に関する解答群
ア dx × x ? dy × y + dx × Vy[2] ? dy × Vx[2]
イ dx × x ? dy × y + dy × Vy[2] ? dx × Vx[2]
ウ dy × x ? dx × y + dx × Vy[2] ? dy × Vx[2]
エ dy × x ? dx × y + dy × Vx[2] ? dx × Vy[2]
オ dy × x ? dx × y + dy × Vy[2] ? dx × Vx[2]
設問2 このプログラムは,描く図形が凸四角形になるかどうかを判定するため,
三つの判定を順番に行っている。
この判定のアルゴリズムに関する次の記述中の  に入れる正しい答えを,解答群の中から選べ。
に入れる正しい答えを,解答群の中から選べ。
(第1の判定)
 のような図形を無効にするため,
P3 と P4 を通る直線の方程式を求めて,P1 と P2 の位置を検査する。
のような図形を無効にするため,
P3 と P4 を通る直線の方程式を求めて,P1 と P2 の位置を検査する。
(第2の判定)
 や
や  のような図形を無効にするため,P4 と P1 を通る直線の方程式を求めて,
P2 と P3 の位置を検査する。
のような図形を無効にするため,P4 と P1 を通る直線の方程式を求めて,
P2 と P3 の位置を検査する。
(第3の判定)
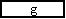 のような図形を無効にするため,
P3 と P1 を通る直線の方程式を求めて,P2 と P4 の位置を検査する。
のような図形を無効にするため,
P3 と P1 を通る直線の方程式を求めて,P2 と P4 の位置を検査する。
解答群
ア 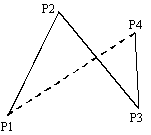 イ
イ 
ウ 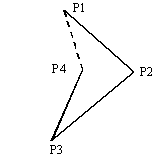 エ
エ 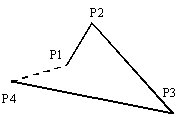
(f、g順不同)
[←前の問題] [次の問題→] [問題一覧表] [分野別] [基本情報技術者試験TOP ]
