
平成30年 春期 基本情報技術者 午前 問02
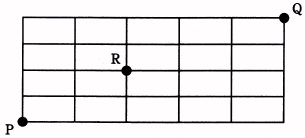
問02 最短経路の組み合わせ図の線上を,点 P から点 R を通って,点 Q に至る最短経路は何通りあるか。
解説
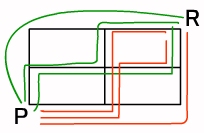 これは、上に2回、右に2回行く4つの組み合わせから2つをとる組み合わせであるから、 4C2=4!/2!(4−2)!=4!/2!×2!= (4×3×2×1)/((2×1)×(2×1))=6 となる。
また、点 R から点 Q に至る最短経路は、同様に、上に2回、右に3回の組み合わせであるから 点 P から点 R を通って,点 Q に至る最短経路は、10×6=60となる。 【平成20年秋 問07】 |
[←前の問題] [次の問題→] [問題一覧表] [分野別] [キーワード索引] [基本情報技術者試験TOP ]
©2004-2025 情報処理試験.jp
|
プライバシーポリシー・著作権・リンク
|
お問合わせ
